Here is another good temperature control and monitoring device STC-3008 integrates two single themperature controllers in this article you will learn how to connect and set ,price and where to buy it, my review.
Here is pros :
- Two two independent temperature controllers in one case
- Red and Blue display
- Two relay a two probes
- Same size as other temperature controllers (for example as MH1210W)
- Have alarm function and delayed start in min
- Al values can set 0.1°C
- Cheap a this price
Here is cons:
- Nothing comes to mind two integrated temperature controller for 10 usd is very cheap
My verdict:
The STC-3008 is a valuable thermostat because at a cost of around 10 usd it gets two universal thermostats in one box. Each thermostat unit can be used separately for cooling or heating.Accuracy is very good to improve it by 0.1°C step calibration. STC-3008 has added alarm function and relay delay in minutes. The connection is similar to other temperature controller as Mh1210W, SHT-2000 more below in the manual…
Its good for hatcheries, terrariums, refrigerators, compressors, for controlling in 2 steps.
Diagram schematic and manual + video
In the rows below I will show you how to connect the STC-3008 as you set it to cool or heat + other functions.Maybe help with the setting my video on youtube – I show there how to set the STC-3008 thermostat for cooling and also for heating:

Heating/cooling mode setting
Setting mode: setting (starting temperature): Press and hold the ▲ button to start the temperature flashing. Use ▲▼ key to set the starting temperature value.
▲” arrow button once to display the starting temperature. Long press the “up ▲” arrow button for about 3 seconds,The required temperature can be set by the up and down keys
Set the stop temperature:
Press the button arrow ▼ once to display the stop temperature. Long press the arrow ▼ button for about 3 seconds and the stop temperature number flashes. The required temperature can be set by the up and down keys
Example in practice:
The first step: heating mode, starting temperature <stop temperature
Step 2: Press and hold the ▲ button to start the temperature flashing. Use ▲▼ to set the starting temperature to 50 °C.
Step 3: Press and hold the ▼ button to stop the temperature flashing. Set the stop temperature to 65 °C with ▲▼ keys, and the setting is completed!
Step 2: Press and hold the ▲ button to start the temperature flashing. Use ▲▼ to set the starting temperature to 30 °C.
The third step: long press the ▼ button to stop the temperature flashing, set the stop temperature to 26 °C by ▲▼, the setting is completed!
Press “Up 1” Button & “Up 2″Button at the same time to setting mode
| Code | Function | Set Range | Default |
| P0 | Compressor 1 delay time | 0-60min | 0min |
| P1 | Compressor delay time | 0-60min | 0min |
| P2 | High temperature alarm value | 55-120° C | 120°C |
| P3 | Low temperature alarm value | 55-120° C | -55°C |
Specification: 
- Display Type: Digital
- Style: Standing Station
Temperature sensor: NTC 10K 3435 - Senor Length: 1.0m
- Temperature measuring range: -55°C ~ 120°C
- Resolution: 0.1°C
- Accuracy:±1°C
- Power supply: 110-220VAC±10%, 50/60Hz
- Power consumption: <3W
- Storage temperature: -30°C ~ 75°C
- Relative humidity: 20% ~ 85% (No condensate)
- Relay contact capacity: Two Relay Cool 10A/240VAC; Heat 10A/240VAC


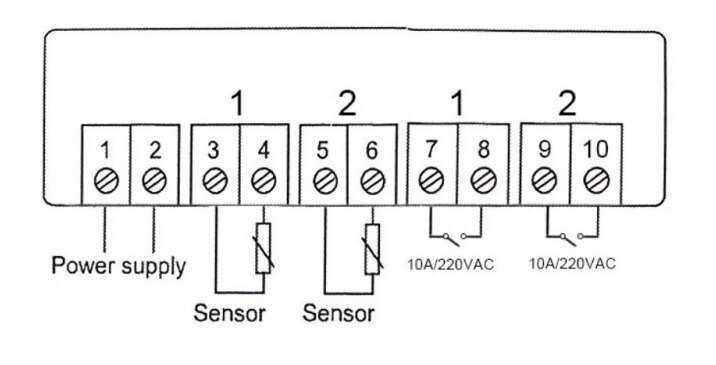








Attachment
I have an STC-3028 but it came with no instructions. The 3008 is similar but only thing the blue display is for humidity. It’s displaying HHH and I’m not able to set it. Can you help?
Check your sensor it might be not tightly attached (or bad)
What is the practical purpose of the delay timer?
timer is good for compressor
I could call
Is a single sensor on both inputs? to get a unique value for both controls?
Hi jackson STC-3008 have two sensors
Do you know of a dual temperature controller that will chose a relay if a difference between the two probes is seen? For example, close relay if the temp in room A is greater than room B by 1deg.
hi adam stc-3008 not suport this thing directly… Stc-3008 is two temperature controllers in one case
Attachment
Hi! The controller shows “LLL LL”. How can I fix it?
sensors not plugged into control unit. or cable cut open circuit
Sir do you have any video or patern on how to wire the stc 3008 for egg incubator??thank you…
Question: on the stc-3008 how do you calibrate the sensor?
-the temperature is out when i measure and i wish to calibrate.
Hello,
2 question.
1st -Question
I need to control 2 fans;
Fan A must only work for temperatures greater than 60 ° C,
Fan B must only work for temperatures greater than 40 ° C,
Then at 34 ° C fan A and fan B will be turned off
at 45 ° C only fan B will be switched on
at 85 ° A and B will be lit.
Can I use the STC-3008 to do this? How ?
2nd Question
Does the thermostat have the CE marking?
Thank you
Yes STC-3008 imagine as two temperature controller in one case
Not have CE marking from Diymore.cc, maybe have from Ketotek
L’STC-3008 SUPPORTA 10A+10A PER UN TOTALE DI 20A O 10A IN TOTALE SULLE DUE USCITE?
Only 10A relay output
Can i used stc 3008 for egg incubator how to installed it
Yes is very good for hatchery or eg incubator
Attachment
Hi Ivan, I need your help wiring 1000w 36V controller. I have one and I am confused about the wiring, you talk about 2 small blue wires, I only have 1.
Please reply, jnj.Kalbar@Hotmail.com
Thanks.
Dear Ivan,
I want to use the STC3008 in my expedition truck to see inside and outside temperatur. I do not need any switching.
On the display on your pictures I see only OUT in blue and OUT in red.
Im looking to control two separate items with controllers, but are conditional upon each other. I want to control the temperature of a room and when the temperature goes above a certain point it turns on my chiller , pump and fans. But I also want a controller to check the temperature of my chiller and when the chiller liquid temperature say reaches 2C it shuts off the chiller compressor until that temperature reaches about 8C. Will the stc-3008 work for something like this, or would I be best to daisy chain two separate controllers where the first one turns on or off the entire system, and the second unit controls only the chiller?
STC3008 work as two intependent temperature controllers , yes can you use in this case
when you set the alarm, does it beep or it flashes?
Attachment
I would like to share some information that might be useful to know. As we could see from the clip and the photos, the display is very bright. In a matter of few days I lost first one segment and a day later another segment from the blue display. The thermostats, I bought STC3008 are 24V rated.
I have examined the device closely and found out major mistakes in the circuit design. The display is wired against any logic:
1. The current limiting resistors are connected to the common cathodes of the display instead of the segments (anodes).
2. The current limiting resistors are only 47 Ohms. This makes the display to operate in much higher current than it is designed for. It operates around 64mA instead of max of 10mA.
With this setup, no display would survive for long time.
3. The power supply arrangement in the unit is also not very good. The design is made for internal 12V operation, and there are added resistors to lower the voltage for the relays that are with 12V coils. This makes the internal voltage to vary from 16V , through 12V and down to 9V depending on how many relays are on at a time.
Interesting findings, I measured a voltage of about 220mV on the 47 Ohm resistors, so that’s about 4.7mA per segment (maybe it’s AC and I measured wrong), but I have the 220v version that’s running internally on ~12v.
Attachment
My device is showing EEE on both sides ?.
Please what does this mean?
Maybee is Error code ” EEE” indicates that the probe sensor is not working properly, if you have correctly plug booth sensor i think you STC-3008 have bug
1. How can I make a 120-240vac unit operate on 12VDC? (I’m using the unit for automotive engine/transmission temperature monitoring).
2. I need to use with 1/8-27 immersion type of sensors. Can you provide such sensors or define the resistance and beta of the sensors used so that I can find a source?
1. can buy 12 VDC version for 10 usd .
2- Sensor is ntc10k can only this type 1/8-27 immersion type mus buy with ntc probe
Hello why this divice is Beeping?
Bonjour J’ai besoin de faire démarrer un ventilateur lorsque la sonde A est >supérieur à B +5° et l’arrêt à B+5°
Le STC 3008 est-il compatible?
Si non, avez-vous un régulateur à proposer?
Mezrci
If you need only switched by temperature diference choose this model
https://usefulldata.com/ewelly-ew-m801ah-temperature-controller-review-and-manual/
Are the relay contacts capable of 10A load?
For example, will a 1200W heating element work with the internal relay ?
the relay is max 10A, but at 8A I would use a contactor
i have stc 3008 wwould like to no does the red light come on as i have pulged ithe heat bleat on and it is getting hot but no red on ,,,, can you use this unit if olny one out let
No it’s not, it’s the same as the STC 1000, which is more simplified with one probe. The STC 3008 can’t keep a certain temperature with one relay, you need the other relay for that purpose as well. I don’t see the use of 2 probes, syncing the 2 relays, just doesn’t make sense. Room temperature for example set at 26, aircon and heater, STC 1000 does that with one probe.STC 3008 needs 2 probes for that.